Heuristic Search

The functional network inference algorithms I work with often involve some sort of heuristic search. Heuristic search is used when it is not possible to calculate an optimal solution to a problem. This usually occurs when the search space—the collection of all possible solutions—is prohibitively large, such that all possible solutions cannot be enumerated, and jagged, meaning that there is no way to follow a smooth path through the search space towards better and better solutions. The quality of a solution is usually defined by some type of score, the details of which depend upon the particular problem. In the following examples, the score is considered to be better if it has a higher value.

I have worked with three types of heuristic search: greedy search, simulated annealing, and genetic algorithms.

Greedy Search

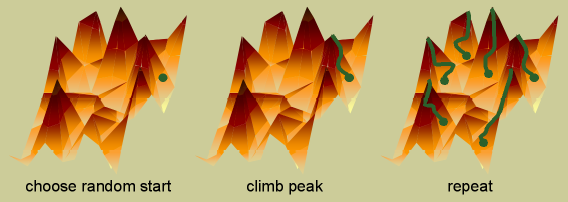
Greedy search consists of starting in random locations in the search space, and only making changes that increase the score. For example, in the case of searching for a network, a random starting point would be defined by randomly selecting edges between nodes (see my brief primer on graphs for an introduction to the terms used here). A change would be an addition or deletion of an edge. When no changes can increase the score (the search has reached a peak in the search space), one round of greedy search is completed. Greedy search is usually performed with a number of random restarts, such that multiple peaks are reached. The highest peak reached over all the restarts is presented as the solution.

Simulated Annealing

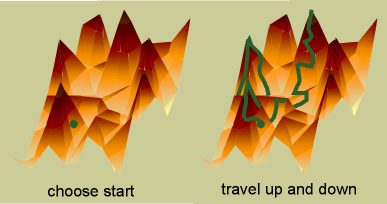
Simulated annealing is the same type of search as greedy search, involving moving in small steps throughout the search space, but is more advanced. Here, one starts either in a random location or a particular defined start place (in networks, this is often the empty graph). The search moves in a series of steps where a change to the solution is proposed (in networks, addition or deletion of an edge). If this change increases the score, it is performed. If it decreases the score, it is performed with a certain probability. This probability slowly decreases throughout the time of the search, such that it eventually reaches zero. At this point simulated annealing is equivalent to greedy search and it climbs the nearest peak. The ability to go back down in score enables a simulated annealing search to visit multiple peaks in one round. The highest peak visited is presented as the solution.

Genetic Algorithms

Genetic algorithms are a different kind of search, based on analogy to biological evolution. A number of different solutions are simultaneously maintained, called a population. The relevant parameters of the solutions are stored as chromosomes, basicially one or more linear orderings of the parameters (in the case of networks, these would be the identity of the edges). The score of a solution is known as its fitness.

The three basic operations in a genetic algorithm are mating, mutation, and selection.

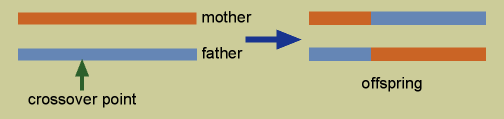
In mating, two solutions (called the mother and father) create two new offspring by crossover of their chromosome. In crossover, a crossover point is randomly chosen in the chromosome. One of the new solutions has the first portion of the chromosome up until the crossover point from the mother, and the remainder from the father. The other new solution has the first part from the father and the remainder from the mother.

In mutation, a random change is made in one of the parameters of the solution.

And in selection, those solutions in the population with the highest fitness are maintained until the next generation, and the remainder are discarded.

A single generation of a genetic algorithm consists of the following:

1. Members of the population mate—mates can either be chosen randomly or on the basis of fitness.
2. Offspring undergo mutation.
3. Selection occurs, and the new population starts the cycle again.

Genetic algorithms are usually run until the mean fitness of the population begins to level off. The member of the population with the highest score is presented as the solution.