Functional Network Inference Algorithms

Functional Networks

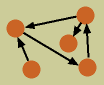functionalnetbkgdTo understand functional network inference algorithms, we must first understand what we mean by a functional network. For the purposes of my research, I define a functional network as the following: A group of variables, which have measurable values, and interact in some way such that the value of one variable affects the value of another. In the image to the left, the variables are represented by circles, and the functional interactions by arrows.

To make it more clear, here are some examples from my research:

gene regulatory network
variables: genes
measurable values: gene expression, measured as mRNA levels on a gene array
interaction:

  • gene expression is taken to correspond to amount of protein product of a gene (note: of course, there may be other factors, as some of my research is attempting to take into consideration; see my Research Page)
  • the amount of transcription factor proteins affects the regulatory influence of a transcription factor on its target; more proteins lead to more activation or suppression
  • this activation or suppression will be reflected in high or low levels of the target gene’s mRNA (the measured gene expression)

Thus, the gene expression of a transcription factor gene influences the gene expression of its target gene.

neural information flow network
variables: brain regions
measurable values: electrophysiological activity, measured through multi-unit extracellular electrodes
interaction:

  • activity in one region corresponds to action potentials traveling down axons of individual neurons to the synapses on neurons in other brain regions
  • neurotransmitters are released in the target brain region, stimulating the target neurons
  • the amount of stimulation received by a neuron influences its likelihood to fire; more stimulation leads to a higher likelihood of firing
  • within a brain region, if a large number of neurons have a higher likelihood of firing, the measured multi-unit activity will be higher

Thus, the measured activity in one brain region influences the measured activity in the target brain region.

Not all the variables and values need to be the same in the functional network, all that is required is that the values are measurable, and that the values of the variables influence each other. For example, an ecological dependence network would have multiple types of variables:

ecological dependence network
variables: (1) species, (2) soil minerals, etc…
measurable values: (1) species abundance, (2) mineral concentration, etc…
interaction:

  • (1) number of predators influences number of prey consumed; thus predator abundance influences prey abundance
  • (2) number of a plant species influences the amount of mineral entire population draws from the soil; thus plant abundance influences mineral concentration
  • etc…

Functional Network Inference Algorithms

alg

I am interested in the case of functional networks when the variables are measured, but the specific network of interactions is unknown. To find this network, I apply functional network inference algorithms.

In general, functional network inference algorithms can be divided into three basic types: pair-wise, equation-based, and network-based:

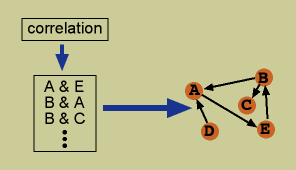pairwisePair-wise algorithms consist of finding pairs of variables whose values are correlated, and suggesting one to putatively influence the other. The process of correlation can be quite complex, using time-lagged correlation, fuzzy logic, or other methods. Many of these algorithms have a cut-off for significance of the correlation or a maximum number of variables another can be connected to in order to limit the interactions found. (References)

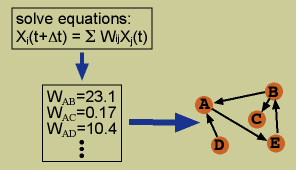equationEquation-based algorithms relate the value of each variable to the value of all other variables in the form of an equation. These equations can be linear, non-linear, and/or differential equations. Putative interactions are identified by solving the set of equations for the weights which relate each variable to the others. These weights represent the influence of each variable on the others. Generally, only a few weights in the equation for a single variable differ considerably from zero and thus are considered putative influencers. (References)

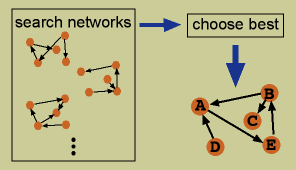netbasedNetwork-based algorithms use a particular network model, most often Boolean networks or Bayesian networks. The best network to describe the data is found, often using a heuristic search method which tries multiple different networks before deciding on a best solution. Boolean networks assume variables only have two states, on and off. Variables are connected to each other with logical relationships, for example: “If variable A is on, then variable B is on”. Logical operations such as “AND” and “OR” can be included in these relationships. A variable included in the “if” portion of such a statement is considered to influence a variable included in the “then” portion. Bayesian networks represent probabilistic connections between variables. An important feature of Bayesian networks is their ability to model conditional independence. For example, if variable A influences variable B, and variable B influences variable C, the values of all three A, B, and C would be correlated. However, a Bayesian network would model that A and C are not connected, because the influence of A to C travels through B. A and C are conditionally independent, conditioned on the variable B. My work thus far has concentrated on using Bayesian networks; see more details about them on my Bayesian Networks Page. (References)

References

I am including these references for those who are interested in learning more about functional network inference. I am not particularly keeping these lists up-to-date, but if you know of a reference that ought to be added, feel free to contact me ([email protected]), and I will try to add it whenever I get around to updating these pages.

Pair-wise algorithms

  • Arkin, A., P. Shen, & J. Ross. 1997. A test case of correlation metric construction of a reaction pathway from measurements. Science 277:1275-1279.
  • Chen, T., V. Filkov, & S. S. Skiena. 1999. Indentifying gene regulatory networks from experimental data. Proceedings of the Annual International Conference on Computational Molecular Biology 3:94-103.
  • Hesse, W., Mšller, E., Arnold, M. & Schack, B. 2003. The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. J. Neurosci. Methods 124, 27-44.
  • Melssen, W.J. & Epping, W.J.M. 1987. Detection and estimation of neural connectivity based on cross correlation. Biol. Cybern. 57, 403-414.
  • Woolf, P. J. & Y. Wang. 2000. A fuzzy logic approach to analyzing gene expression data. Physiological Genomics 3:9-15.

Equation-based algorithms

  • Baccalá, L.A. & Sameshima, K. 2001. Partial directed coherence: a new concept in neural structure determination. Biol. Cybern. 84, 463-474.
  • Chen, T., H. L. He, & G. M. Church. 1999. Modeling gene expression with differential equations. Pacific Symposium on Biocomputing 4:29-40.
  • D’haeseleer, P., X. Wen, S. Fuhrman, & R. Somogyi. 1999. Linear modeliing of mRNA expression levels during CNS development and injury. Pacific Symposium on Biocomputing 4:41-52.
  • Rosenberg, J.R., Halliday, D.M., Breeze, P. & Conway, B.A. 1998. Identification of patterns of neuronal connectivityÑpartial spectra, partial coherence, and neuronal interactions. J. Neurosci. Methods 83, 57-72.
  • Weaver, D. C., C. T. Workman, & G. D. Stormo. 1999. Modeling regulatory networks with weight matrices. Pacific Symposium on Biocomputing 4:112-123.

Network-based algorithms

  • Akutsu, T. S. Miyano, & S. Kuhara. 1999. Identification of genetic networks from a small number of gene expression patterns under the boolean network model. Pacific Symposium on Biocomputing 4:17-28.
  • Akutsu, T. S. Miyano, & S. Kuhara. 2000. Algorithms for identifying boolean networks and related biological networks based on matrix multiplication and fingerprint funciton. Proceedings of the Annual International Conference on Computational Molecular Biology 4:8-14.
  • Akutsu, T. S. Miyano, & S. Kuhara. 2000. Algorithms for inferring qualitative models of biological networks. Pacific Symposium on Biocomputing 5:290-301.
  • Friedman, N., M. Linial, I. Nachman, & D. Pe’er. 2000. Using bayesian networks to analyze expression data. Journal of Computational Biology 7:601-620.
  • Hartemink, A.J., D.K. Clifford, T.S. Jaakola, R.A. Young. 2001. Using graphical models and genomic expression data to stastically validate models of genetic regulatory networks. Pacific Symposium on Biocomputing 6:422-433.
  • Hartemink, A.J., D.K. Clifford, T.S. Jaakola, R.A. Young. 2002. Combining location and expresion data for principled discovery of genetic regulatory network models. Pacific Symposium on Biocomputing 7:437-449.
  • Liang, S., S. Fuhrman, & R. Somogyi. 1998. REVEAL, a general reverse engineering algorithm for inference of genetic network architectures. Pacific Symposium on Biocomputing 3:18-29.
  • Mjolsness, E., T. Mann, R. Castaño, & B. Wold. 2000. From coexpression to coregulation: an approach to inferring transcriptional regulation among gene classes from large-scale expression data. In: Advances in Neural Information Processing Systems 12, S. A. Solla, T. K. Leen, & K. R. Muller (eds). Cambridge, MA: MIT Press, pp. 928-934.
  • Thieffry, D. & R. Thomas. 1998. Qualitative analysis of gene networks. Pacific Symposium on Biocomputing 3:77-89.

Cookie preferences